マイクロマウス迷路の自動生成
概要
こんにちは。けりです。
マイクロマウスを作るにあたり、 普段は迷路を解くことばかり考えていますが、 今回はその迷路を作成するお話です。
試してみたのは、 ランダムウォークによる迷路の自動生成です。
果たしてマイクロマウスっぽい迷路はできるのでしょうか?
迷路生成アルゴリズム
実は、マイクロマウスに限らなければ、 迷路の自動生成アルゴリズムは代表的なものがいくつか存在します。
そこで、今回は以下の迷路生成アルゴリズムを試してみました。
- 棒倒し法
- 穴掘り法
- 穴掘り法の独自拡張
棒倒し法
まずはじめに一番簡単な方法です。
迷路上のすべての柱から無作為に棒を倒すように壁を立てる方法によって迷路を作ることができます。
とても簡単なアルゴリズムですが、 すべての柱に少なくともひとつの壁が隣接しているようなマイクロマウス規定に則った迷路が作成できます。
自動生成された迷路
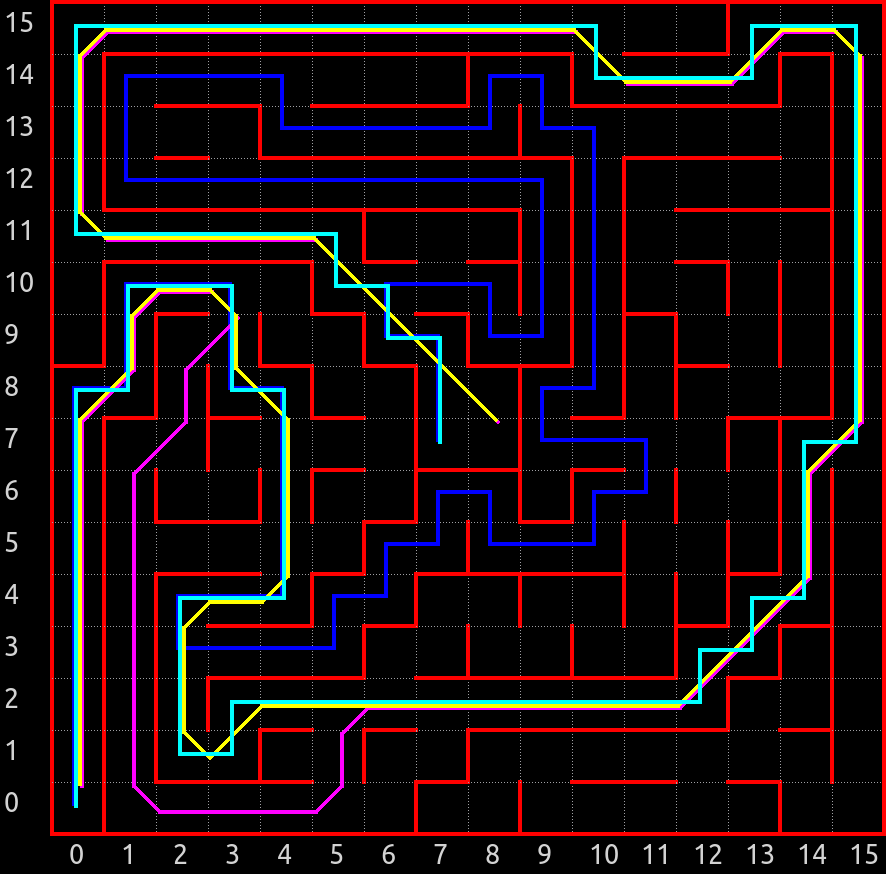
棒倒し法によって次のような迷路が自動生成されました。
乱数なので、実行するたびに全く違う迷路が生成されます。
何通りか生成して、 複数のルートが現れるものを選びました。
ゴール区画の選択
今回の迷路では、 ゴール区画は スタート区画から行き得る最も遠い区画に設定しました。
具体的には、スタート区画からステップマップを展開した際に一番ステップが大きくなる区画です。
簡単のため、今回は1マスのゴールとしています。
最短経路の種類
区画および壁ベースの歩数最短と、スラロームと台形加速を考慮した斜めありなしの時間最短の経路を表示しています。
| 色 | アルゴリズム |
|---|---|
| 青色 | 区画ベースの歩数最短 |
| マゼンタ | 壁ベースの歩数最短 |
| 黄色 | スラロームと台形加速を考慮した時間最短(斜めあり) |
| シアン | スラロームと台形加速を考慮した時間最短(斜めなし) |
迷路の考察
あまり複雑な最短経路はできず、だいたい単純な最短経路のみです。
また、封鎖されている区画が多く目立ちます。 運が悪いとスタート区画付近が封鎖されて、つまらない迷路になってしまいます。
このアルゴリズムではあまりいい迷路はできそうにありません。
穴掘り法
次に、ランダムウォークによる迷路生成アルゴリズムを試しました。
穴掘り法とは、 予め迷路内のすべての壁を立てた状態にして、 スタート区画から壁を消しながらランダムウォークで進んでいく方法です。
このとき、すべての移動をランダムウォークとするのではなく、 未訪問の区画をなくすため、 深さ優先探索アルゴリズムがしばしば用いられます。
具体的には、 先に進む際に現在位置をスタック配列に保管し、 周囲が既知区画になったらスタックを辿って未知区画に隣接したところまで戻り ランダムウォークを再開するという流れです。
深さ優先探索ランダムウォークを用いることで、 棒倒し法のときのような閉鎖空間がなく、 すべての区画に到達可能な迷路ができるという特徴があります。
また、すべての柱に少なくとも1つの壁が隣接している、 マイクロマウス規定に則った迷路が生成できます。
自動生成された迷路
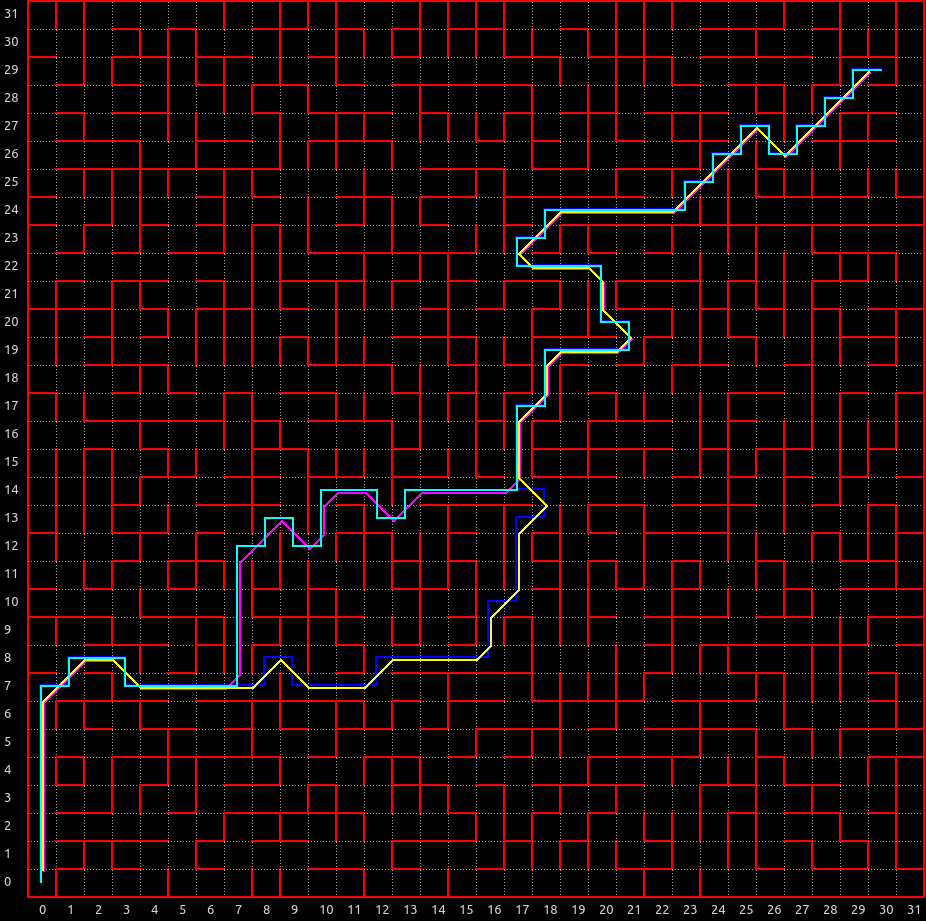
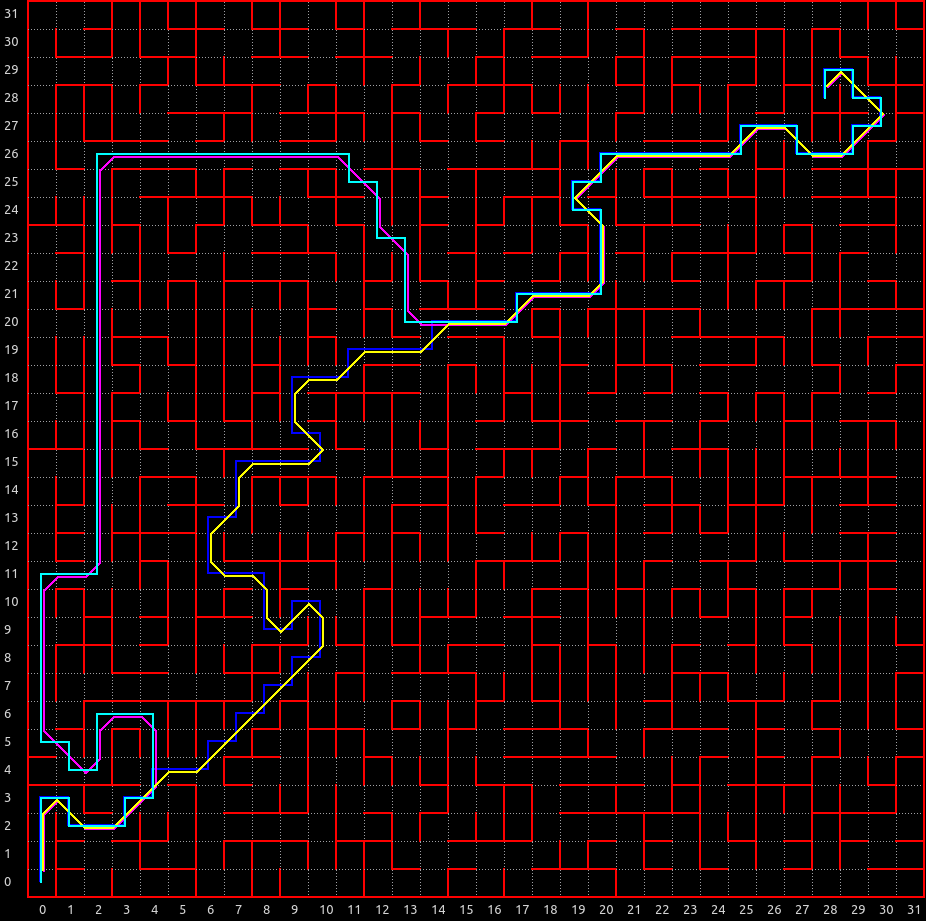
深さ優先探索ランダムウォークの穴掘り法によって 次のような迷路が自動生成されました。



迷路の考察
棒倒し法で生成された迷路とは性質が全くことなることがわかります。
迷路全体を通るスパルタ経路ができがちです。
これが最短経路とはとても思えないくらいの長距離迷路です。
(まるで中部地区大会のようですね)
実は、この迷路にはもう一つ特徴があります。
スタートを根とした 木構造 になっており、 適当な2点間の経路が必ず一意になるというものです。
したがって、スタートからゴールのルートも1通りしかありません。
マイクロマウスでは複数のルートからマシンにあったルートを選択するところもおもしろいところなので、 それができなくなってしまうのはイマイチです。
深さ優先探索ランダムウォークの独自拡張
最後に私が独自に拡張した迷路生成アルゴリズムの紹介です。
木構造を崩す
前述の通り、木構造の迷路ではルートが一意に定まってしまうので、 ルート選択の楽しみがなくなってしまいます。
そこで、上述の深さ優先探索ランダムウォークアルゴリズムを拡張して、 既知区画に囲まれた状態になったとき、 スタックを遡る前に、 前方の壁を ある程度の確率でなくす という動作を追加しました。
その結果、いくつもルートが存在するようなマイクロマウスらしい迷路の生成に成功しました。
直線に重みをつける
マイクロマウスといえば、直線の加速が魅力的です。
しかしながら、ランダムウォークで作成した迷路はどうしてもくねくねした道になりがちです。
そこで、 ランダムウォークで方向を決定する際に、直進と右左折の確率分布を調整して、 直線が多くなるように誘導しました。
同様に、斜め直線が多くなるように、右→左→右→左というルートもできやすくしました。
自動生成された迷路
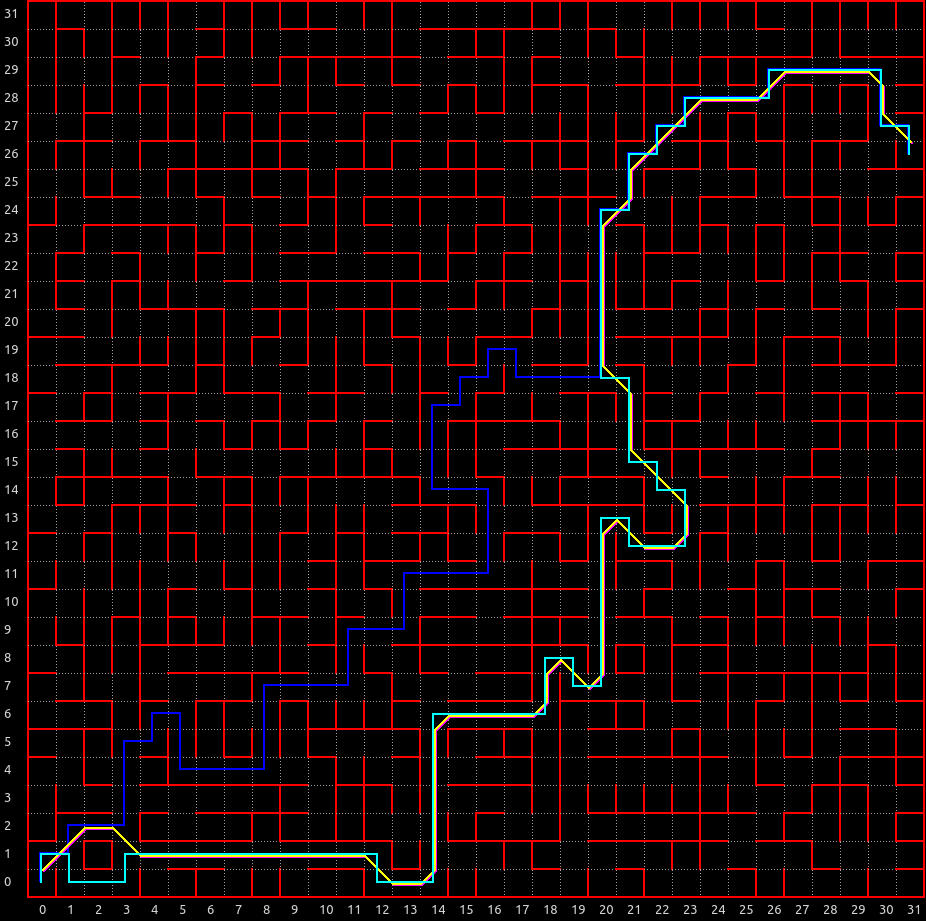
さて、 深さ優先探索ランダムウォークの独自拡張によって 次のような迷路が自動生成されました。
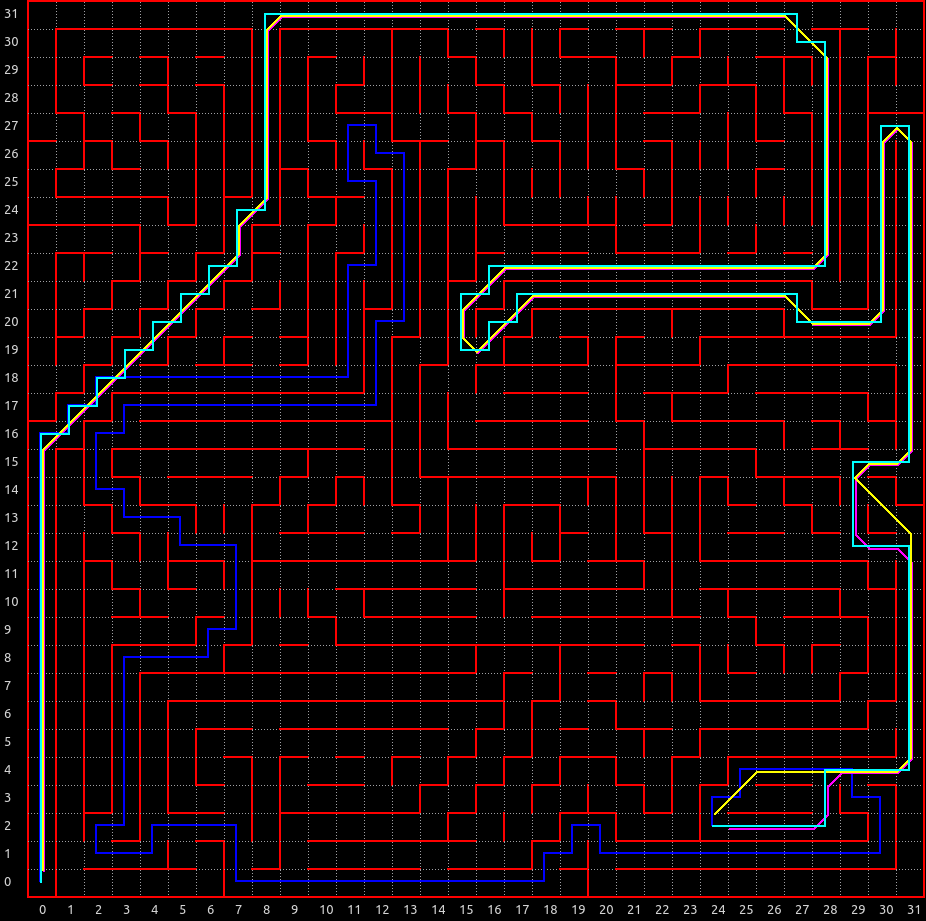
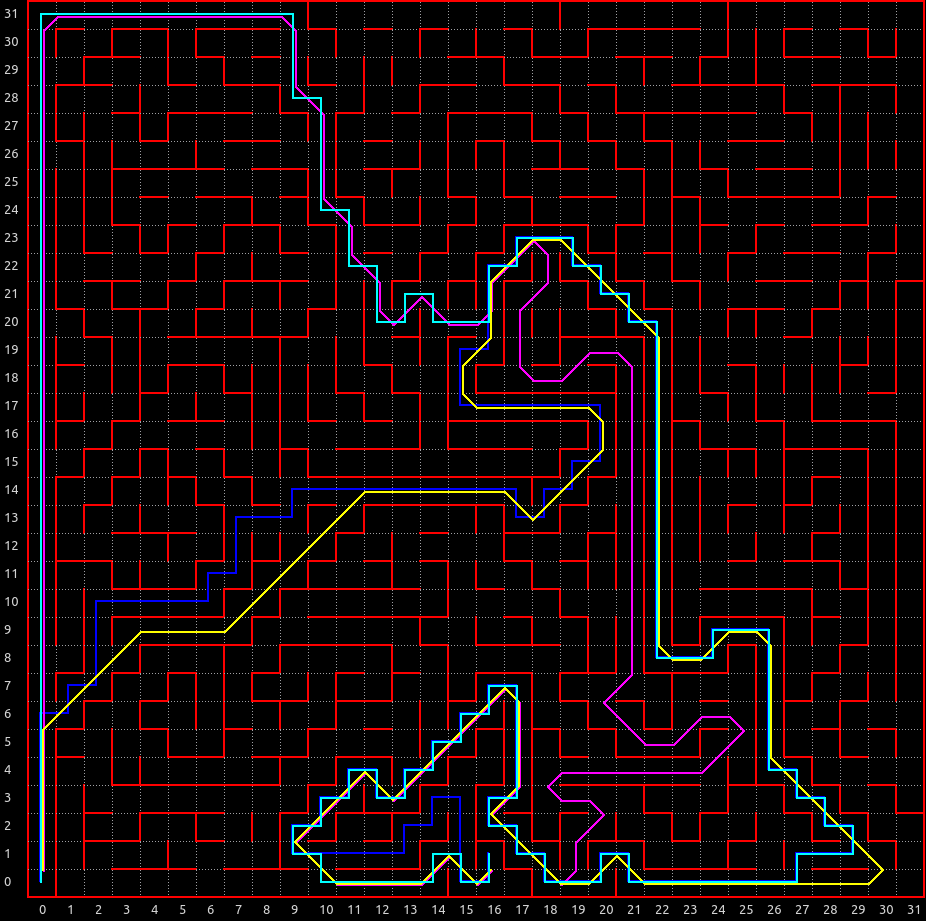
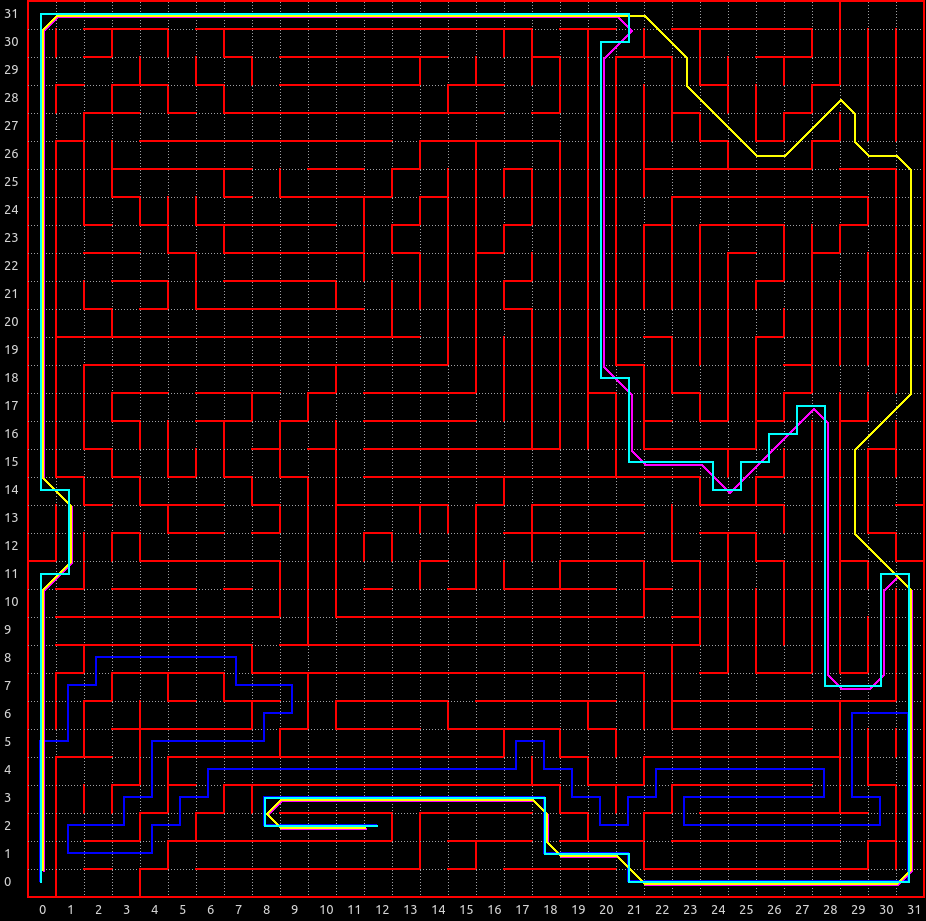
乱数でいくつか生成して、複数のルートができたものを掲示しています。
迷路の考察
複数のルートがあり、 斜め直線が魅力的なマイクロマウスっぽい迷路になっていることがわかります。
確率分布をいじることで、 行き止まりや直線の量なども調整できて結構恣意的な迷路を作ることができました。
競技用の課題迷路を作ってみた
せっかくなので、実際に競技で使えそうな32x32の課題迷路をひとつ作成してみました。
上記アルゴリズムによって自動生成して、適当にゴール区画を3x3区画に直したものです。

この迷路ファイルのダウンロードはこちら。 最短経路の例はこちら。
どうですか?マイクロマウスっぽい迷路ですよね!
まとめ
今回の記事ではマイクロマウス迷路の自動生成について紹介しました。
いかにマウスっぽい迷路を作るか。おもしろいところです。
以前、マイクロマウス運営の方が「毎年迷路を作るのが結構大変」と話していたので、 この方法が役立つかもしれません。
最初自動生成で雛形を作って、そのあと人間が調整するとさらにいい迷路ができそうです。
ちなみに、 この方法を使えば、 64x64の迷路とかも簡単に生成できてしまいます。 恐ろしいですね…
まさか、クオータサイズクラスで64x64迷路の競技なんて開催されるわけないですよね?
それではまた!
