なめらかな加速の設計③ 走行距離を考慮した速度設計

設計2・走行距離を考慮した速度設計

前回の記事の続きです。

この記事では、設計1の曲線加速を組み合わせて、走行距離を考慮した速度設計について考えます。

なめらかな加速の設計 目次

• なめらかな加速の設計① 台形加速と曲線加速
• なめらかな加速の設計② 曲線加速の設計
• なめらかな加速の設計③ 走行距離を考慮した速度設計
• なめらかな加速の設計④ C++による実装例

設計内容

設計1によって、始点速度と終点速度を与えれば、それを繋ぐ曲線加速を生成できるようになりました。

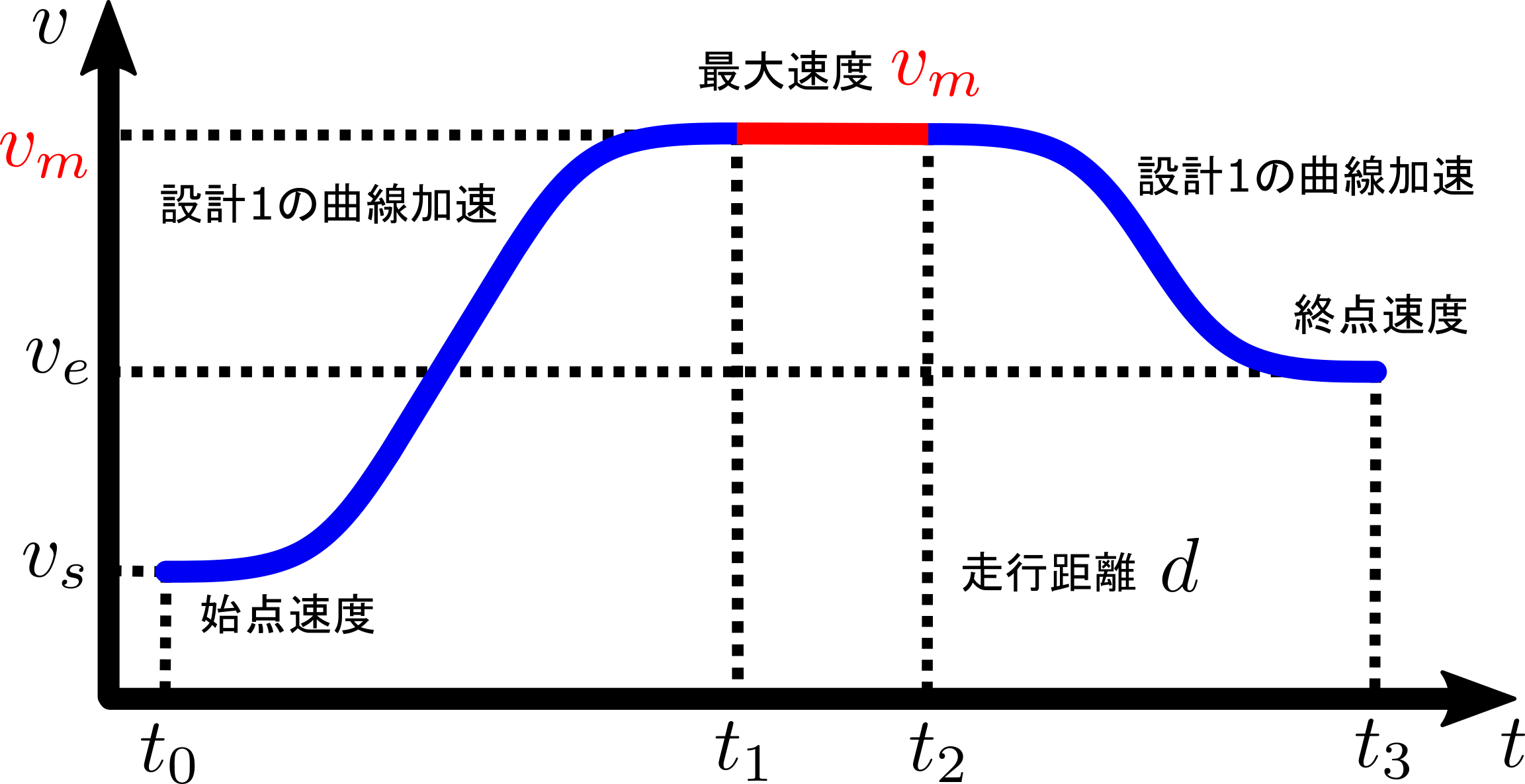
今度はそれを組み合わせて、始点速度→加速→最大速度→減速→終点速度、というような速度軌道を設計します。

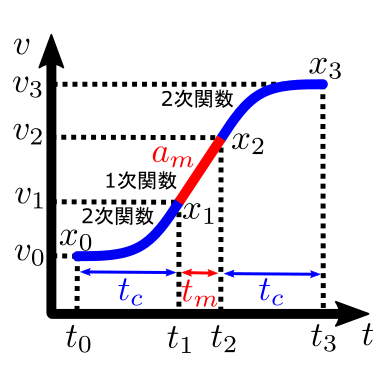
ここで、図中の赤線である最大速度とその継続時間は、走行距離の拘束条件を満たすように算出します。

拘束条件

与える情報は以下の通りです。

• 最大躍度 $j_\max$
• 最大加速度 $a_\max$
• 始点速度 $v_{s}$
• 飽和速度 $v_{a}$
• 目標速度 $v_{t}$
• 走行距離 $d$

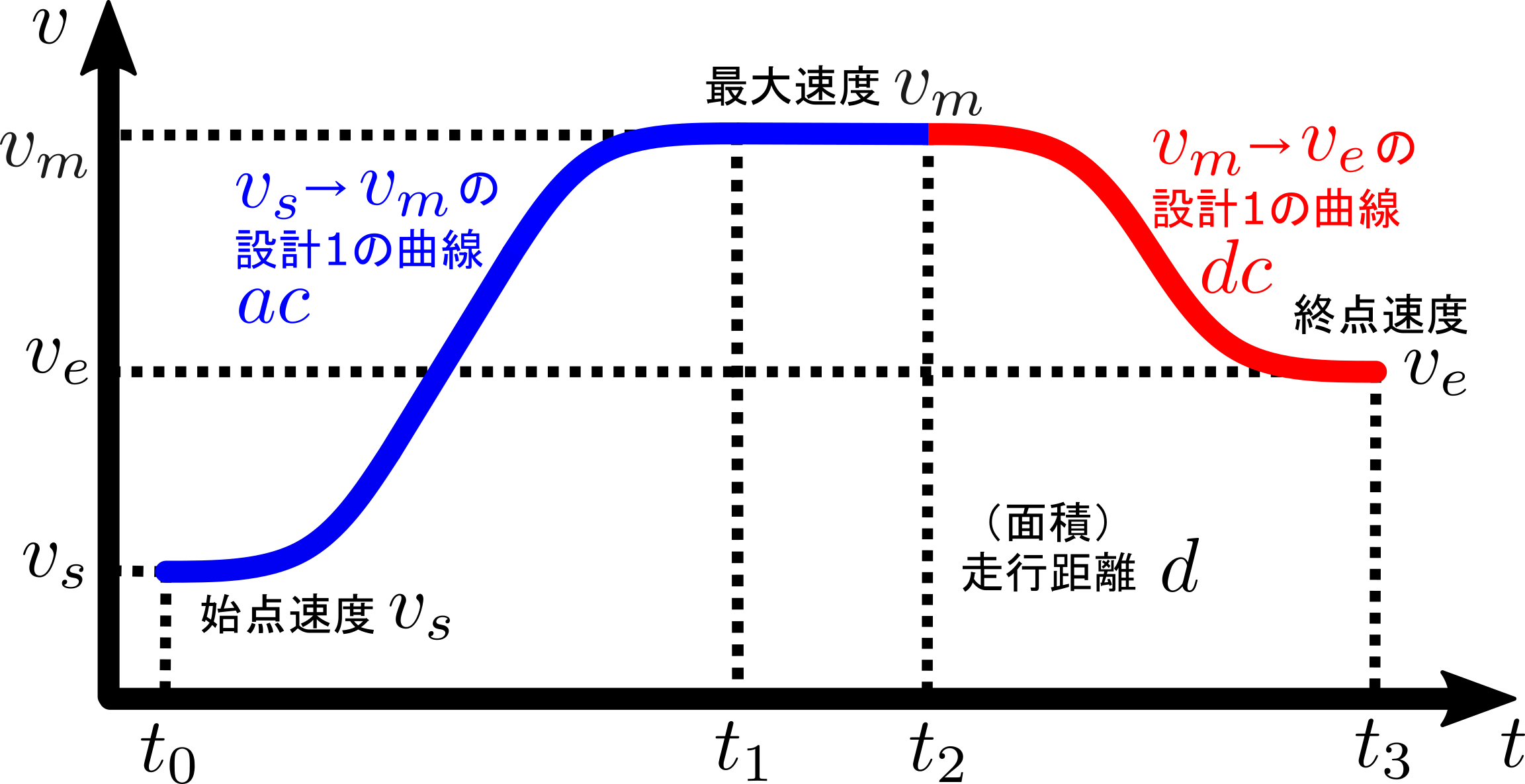
設計1との違い

前回の設計1と比べて、飽和速度 $v_a$ と走行距離 $d$ が新たに加わりました。

また、終点速度 $v_e$ という名前だった速度が目標速度 $v_t$ という名前に変わりました。

というのも、走行距離 $d$ と最大加速度 $a_m$ などの拘束条件により、与えられた目標速度 $v_t$ に達することができない場合があるからです。

したがって、結果的に算出される終点速度 $v_e$ は、目標速度と $v_t$ と異なる場合があるので注意します。

導出結果

設計2では、次のような式を求めました。

• 走行距離などの拘束条件から終点速度 $v_e$ を求める式
• 走行距離などの拘束条件から最大速度 $v_m$ を求める式
• 任意の時刻 $t$ における、躍度 $j(t)$, 加速度 $a(t)$、速度 $v(t)$, 位置 $x(t)$

それぞれについて以下で説明します。

走行距離の拘束から終点速度$v_e$を求める式

与えられた拘束条件から終点速度を求める式です。

$$ \begin{align} v_e(t_c, a_m, v_s, v_t, d) &:= \left\{\begin{array}{ll} v_{e1} & (d \ge d_m) \newline v_{e2} & (d < d_m) \end{array}\right. \end{align} $$

ただし、

$$ \begin{align} d_m &:= 2 v_s t_c + a_m t_c^2 \newline v_{e1} &:= \frac{-a_m t_c + \sqrt{a_m^2 t_c^2-4(a_m t_c v_s - v_s^2 - 2a_m d)}}{2} \newline v_{e2} &:= \frac{1}{3}\left(c +\frac{4a^2}{c} -a \right) \newline a &:= v_s \newline b &:= \frac{a_md^2}{t_c} \newline c &:= \sqrt[3]{\frac{\sqrt{27b(32a^3+27b)} + 16a^3+27b}{2}} \end{align} $$

少し複雑になってしまいましたが、一応これで求めることができます。

注意点として、$v_{e2}$の計算する際、減速の場合、2乗根の中身が負になる場合があるので、この部分の計算は複素数で行う必要があります。

答えは必ず実数になるので、どうにか実数で計算できないか考えましたが、今のところ解決策は見つかっていません。

走行距離などから最大速度$v_m$を求める式

与えられた拘束条件から最大速度を求める式です。

$$ \begin{align} v_m(t_c, a_m, v_s, v_a, v_e, d) &:= \min\{v_a,~v_{m2}\} \end{align} $$ ただし、 $$ \begin{align} v_{m2} &:= \max\{v_s, v_e, v_{m1}\} \newline v_{m1} &:= \frac{-a_mt_c + \sqrt{a_m^2t_c^2-(v_s+v_e)a_mt_c+4a_md+2(v_s^2+v_e^2)}}{2} \end{align} $$

任意の時刻における、加速度、速度および位置

ここままで与えられた、もしくは算出した下記パラメータを用いて設計1の曲線加速を組み合わせます。

• 始点速度 $v_{s}$
• 最大速度 $v_{m}$
• 終点速度 $v_{e}$
• 走行距離 $d$

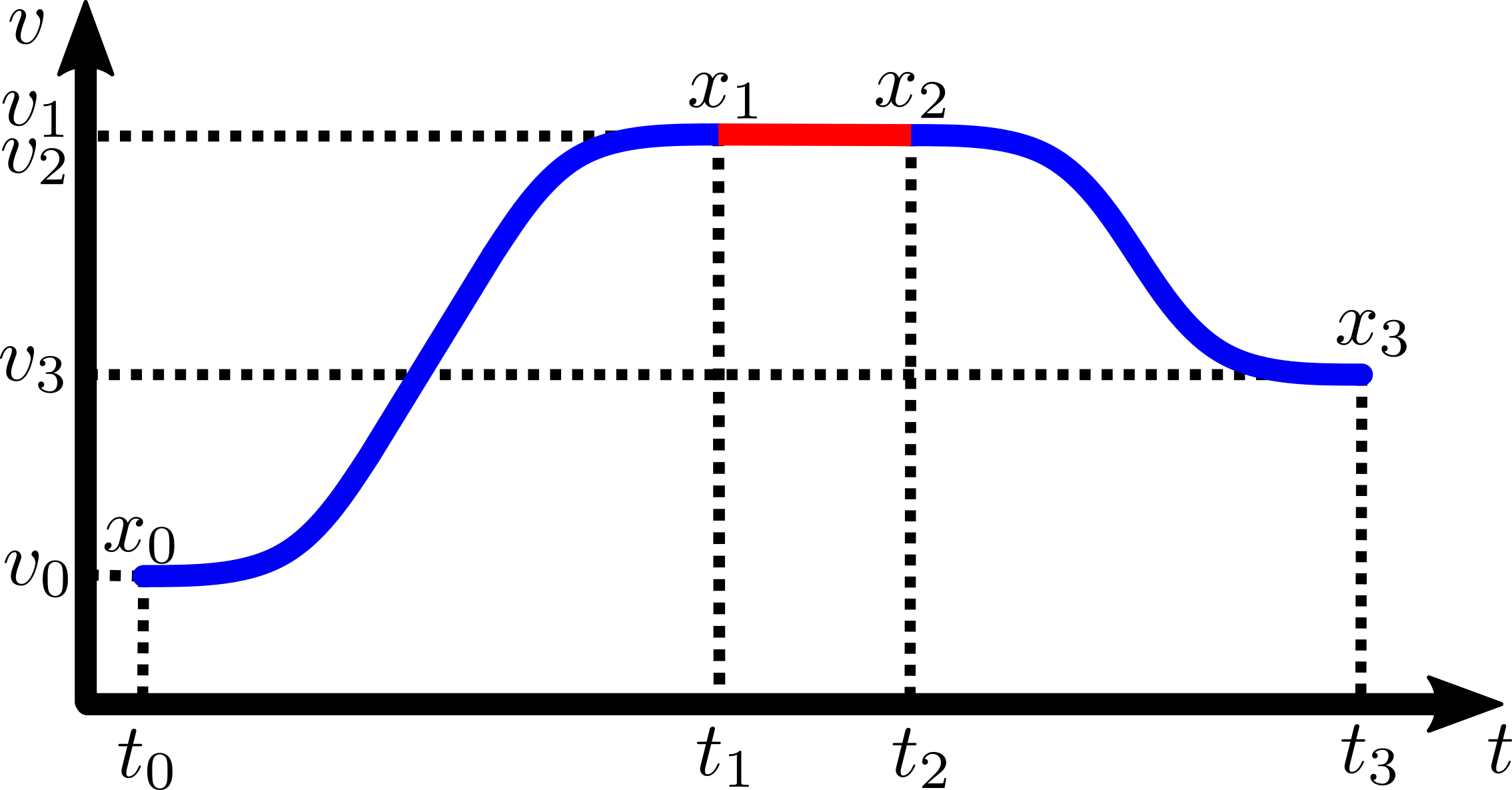
前回の記事で設計した設計1の曲線加速に対して、

• 始点速度を$v_s$
• 終点速度を$\color{red}{v_m}$

としたものを加速曲線 $ac$、

• 始点速度を$\color{red}{v_m}$
• 終点速度を$v_e$

としたものを減速曲線 $dc$として定義します。

このとき、減速曲線 $dc$ の方は、上図の通り $t_2 $だけ時間をシフトした形で使用します。

各境界点時刻の定義は、以下の通りです。

$$ \begin{align} t_0 &:= 0 \newline t_1 &:= ac.t_{end} \newline t_2 &:= t_1 + \frac{d - ac.x_{end} - dc.x_{end}}{v_m} \newline t_3 &:= t_2 + dc.t_{end} \end{align} $$

導出過程

走行距離などから終点速度を求める式

走行距離$d$がある程度小さいとき、与えられた拘束条件では目標速度$v_t$にたどり着けない場合があります。

ここでは、そのような場合にギリギリたどり着ける終点速度$v_e$を求めます。

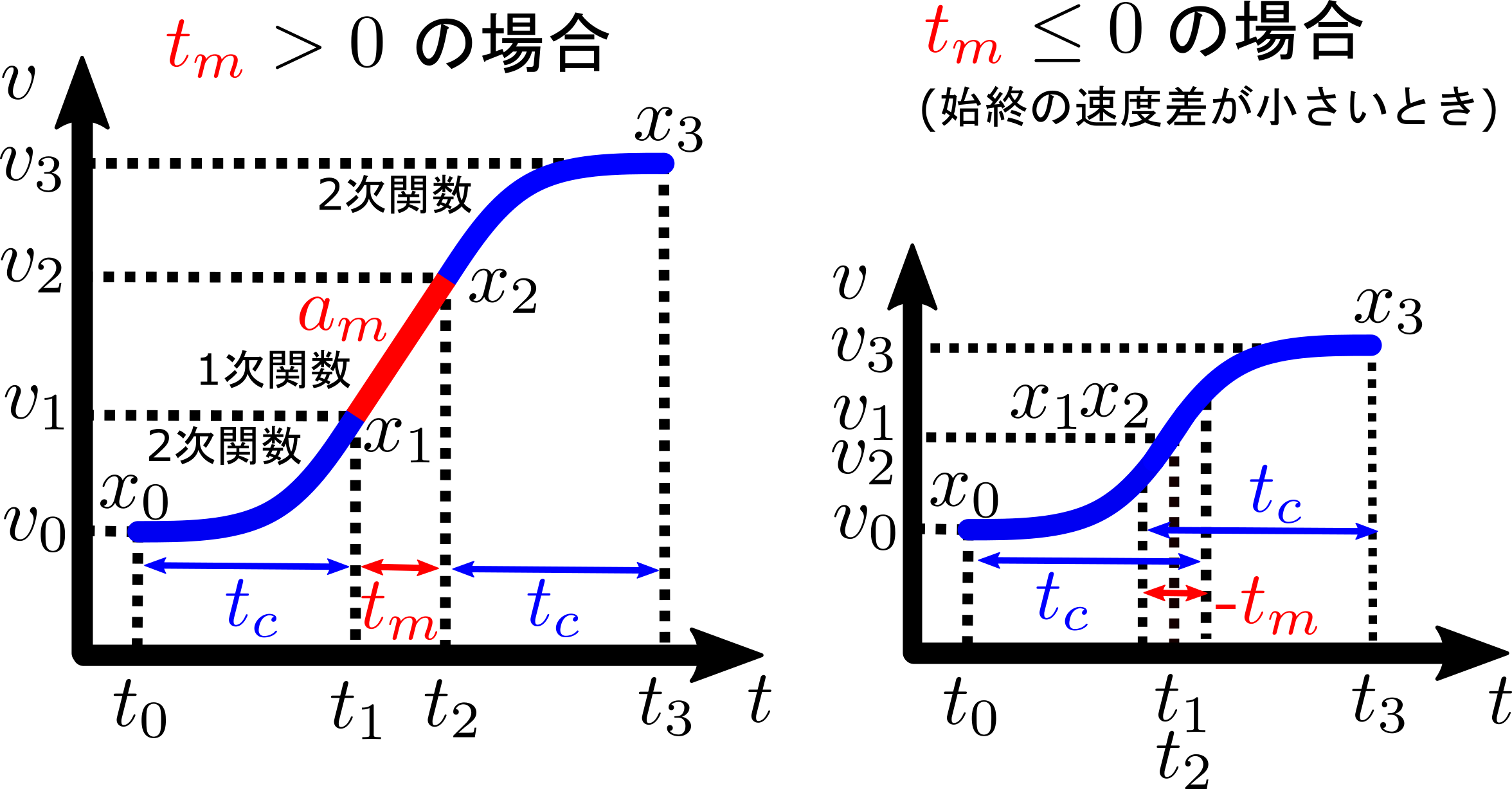
例によって、上図のように、走行距離$d$の大きさによって等加速度の時間$t_m$の有無が変わるので場合分けが必要です。

そこで、$t_m=0$となる走行距離$d_m$を求めます。

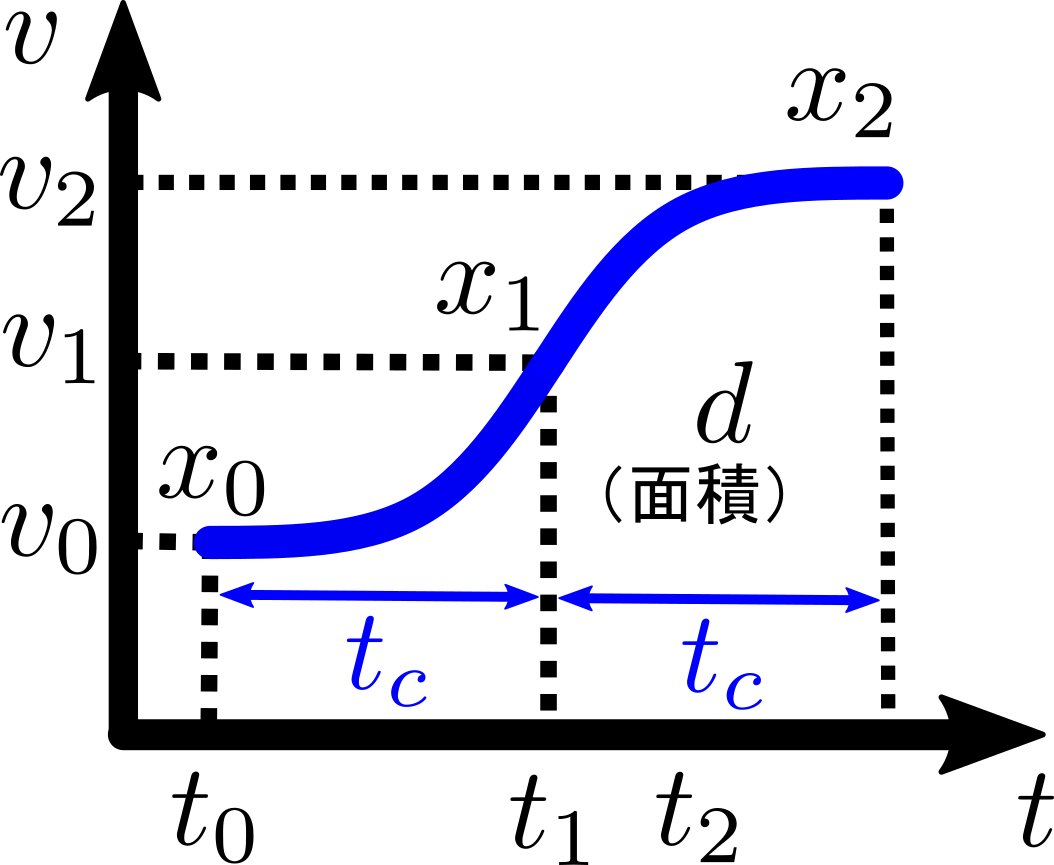
図の曲線の数式を積分して面積を求めます。

$$ \begin{align} d_m & = \int_{t_0}^{t_1}v(t) dt + \int_{t_1}^{t_2}v(t) dt \newline &= \int_{t_0}^{t_1}\left( v_0+\frac{1}{2} j_m(t-t_0)^2 \right) dt \newline &\quad+ \int_{t_1}^{t_2}\left( v_0+\frac{1}{2} j_m(t_1-t_0)^2 +j_m(t_1-t_0)(t-t_1) - \frac{1}{2}j_m(t-t_1)^2 \right) dt \newline &= 2v_0t_c+a_mt_c^2 \end{align} $$

ただし、最大躍度$j_m:=a_m/t_c$を用いました。

このあとは、走行距離$d$が$d_m$より大きいか小さいかで場合分けをして、終端速度$v_e$を求めます。

$d\ge d_m$のとき

$d\ge d_m$のとき、$t_m \ge 0$となります。

求める終点速度を$v_{e1}$とおくと、 曲線の対称性により、台形の面積の公式を用いて、

$$ \begin{align} d &= \frac{1}{2}(v_s+v_{e1})(t_3-t_0) \newline &= \frac{1}{2}(v_s+v_{e1})(t_c+t_m+t_c) \newline &= \frac{1}{2}(v_s+v_{e1})\left(t_c+\frac{v_{e1}-v_s}{a_m}\right) \newline \Leftrightarrow v_{e1} &= \frac{1}{2}\left(\sqrt{4v_s^2-4v_sa_mt_c+a_m(a_mt_c^2+8d)}-a_mt_c\right) \end{align} $$

$d < d_m$のとき

$d < d_m$のとき、$t_m < 0$となります。

求める終点速度を$v_{e2}$とおくと、 曲線の対称性により、台形の面積の公式を用いて、

$$ \begin{align} d &= \frac{1}{2}(v_s+v_{e2})(t_3-t_0) \newline &= \frac{1}{2}(v_s+v_{e2})2\sqrt{\frac{t_c}{a_m}(v_{e2}-v_s)} \newline \Leftrightarrow v_{e2}^3 &+ v_s v_{e2}^2-v_s^2v_{e2}-v_s^3-\frac{a_md^2}{t_c} = 0 \newline \Leftrightarrow v_{e2} &= \frac{1}{3}\left(c +\frac{4a^2}{c} -a \right) \newline a &:= v_s \newline b &:= \frac{a_md^2}{t_c} \newline c &:= \sqrt[3]{\frac{\sqrt{27b(32a^3+27b)} + 16a^3+27b}{2}} \end{align} $$

以上をまとめると、たどり着き得る終点速度$v_{e1}$は、

$$ \begin{align} v_{e} &:= \left\{\begin{array}{ll} v_{e1} & (d \ge d_m) \newline v_{e2} & (d < d_m) \end{array}\right. \end{align} $$

これで、走行距離から逆算した終点速度$v_e$が求まりました。

走行距離などから最大速度を求める式

次に、下図のように走行するために、最大速度$v_m$を求めます。

まずはじめに、飽和速度$v_a$は考えずに、始点速度$v_s$から最大速度$v_{m1}$に達して終点速度$v_e$に達する下図の場合を考えます。

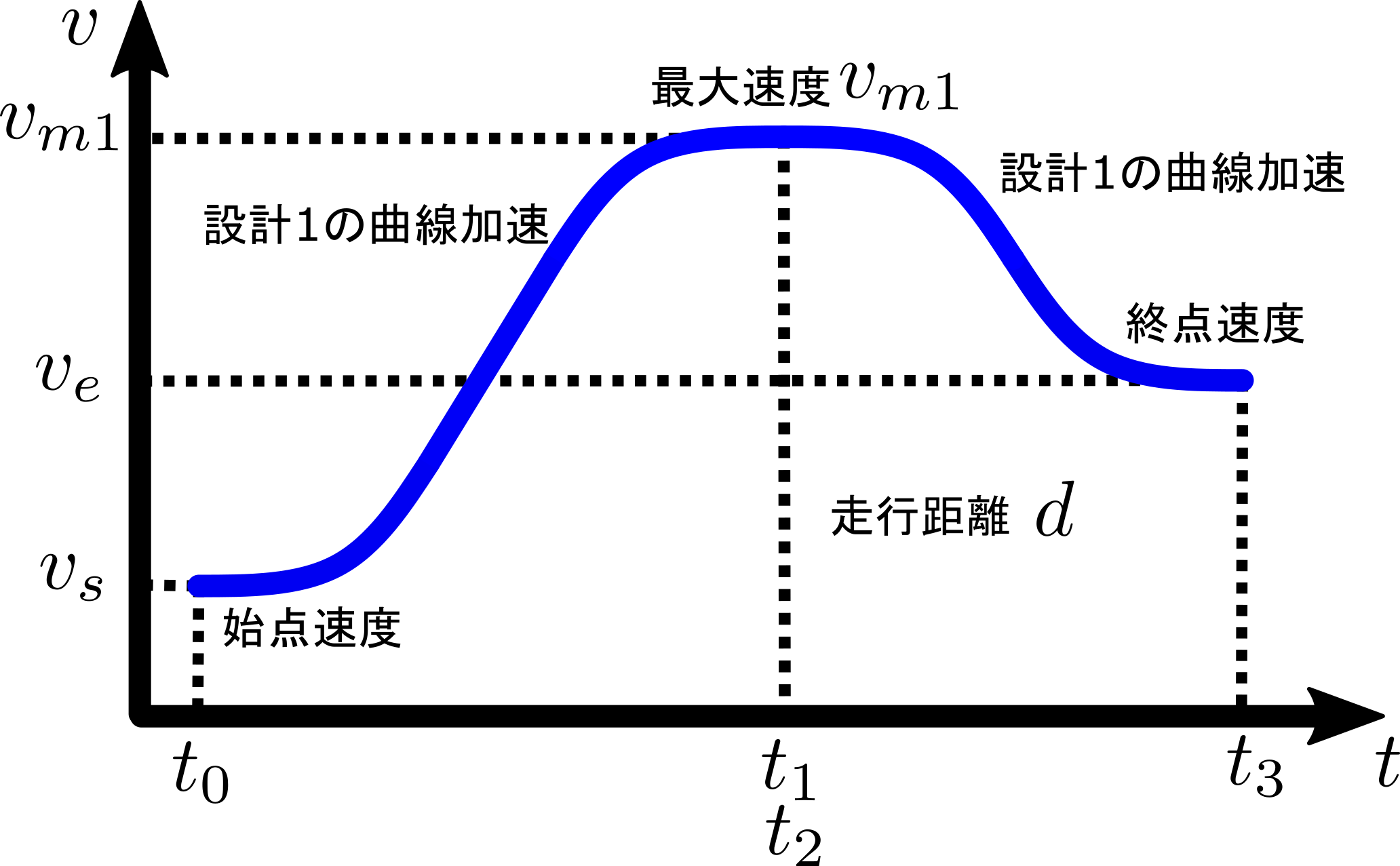
その間の走行距離が$d$となることから$v_{m1}$求めると以下が得られます。

$$ \begin{align} d &= \frac{1}{2}(v_s+v_{m1})(t_1-t_0)+ \frac{1}{2}(v_{m1}+v_e)(t_3-t_2) \newline &= \frac{1}{2}(v_s+v_{m1})\left(t_c+\frac{v_{m1}-v_s}{a_m}\right)+ \frac{1}{2}(v_{m1}+v_e)\left(t_c+\frac{v_e-v_{m1}}{a_m}\right) \newline \Leftrightarrow v_{m1} &:= \frac{-a_mt_c + \sqrt{a_m^2t_c^2-(v_s+v_e)a_mt_c+4a_md+2(v_s^2+v_e^2)}}{2} \end{align} $$

ここで、無駄な減速を避けるため、以下の式で飽和します。

$$ \begin{align} v_{m2} &:= \max\{v_s,~v_e,~v_{m1}\} \end{align} $$

最後に、最大速度$v_m$は、飽和速度$v_a$を超えてはならないので、それで飽和させます。

$$ \begin{align} v_m = \min\{v_a,~v_{m2}\} \end{align} $$

これで、下図のように走行する最大速度$v_m$が求まりました。

まとめ

本記事では、走行距離の拘束条件を満たすような曲線加速を設計しました。

次回の記事では、そのためのC++実装例を紹介します。