なめらかな加速の設計① 台形加速と曲線加速
概要
今回はマイクロマウスにおける速度設計のお話です。
長い直線などを走行するとき、タイムを縮めるため、最大速度まで加速して、ターン直前に減速します。
ここで注意したのが、途中経過の如何にかかわらず、終点の位置や速度は守らなければならないということです。
今回の記事では、終点位置、終点速度や最大速度などの拘束条件から、走行途中の速度軌道を算出するアルゴリズムを紹介します。
最後にはC++での実装したクラスも簡単に紹介します。
なめらかな加速の設計 目次
台形加速の問題点
よく使われる速度設計として、台形加速があります。
加速 → 等速 → 減速 に対して速度のグラフを描くと台形になるので、台形加速と呼ばれます。
台形加速のグラフ
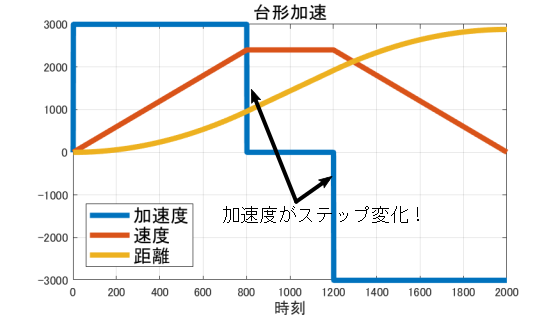
しかしながら、台形加速の場合、速度の微分である加速度はステップ変化しています。
これは、車体に対して急に力を加えるのと同じことになり、クラッシュしてしまうかもしれません。
この問題を解決するために、加速度の変化を連続にして、なめらかに加速するのが曲線加速です。
曲線加速のグラフ
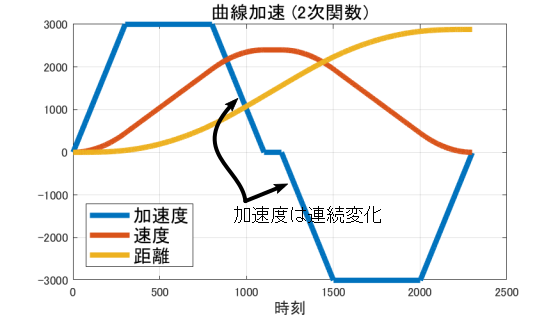
今回の記事では、このような曲線加速の速度設計について考えていきます。
関数の選択
曲線加速を設計するとき、どのような曲線の関数を選ぶか、という問題があります。
本来ならば、無限回微分をしても連続性を保つ、
- 三角関数 $\sin(\omega t)$
- 指数関数 $\exp(\omega t)$
を使いたいところです。
しかしながら、これらの関数の場合、移動距離から走行速度を 逆算 しようとしたとき、方程式が解けなくなるという問題があります。
そこで今回は、
- 加速度を 1次関数
- 速度を 2次関数
- 位置を 3次関数
としました。
これならば、位置から速度を逆算する際の方程式は3次なので、解の公式を使って解くことができます。
設計方針
さて、設計方法をわかりやすくするために、次のように2つの段階にわけて曲線の設計を行います。
設計1
まずはじめに、与えられた始点速度から終点速度までをなめらかにつなぐ曲線を設計します。
ここでは位置による拘束条件は考えません。
設計1 加速曲線
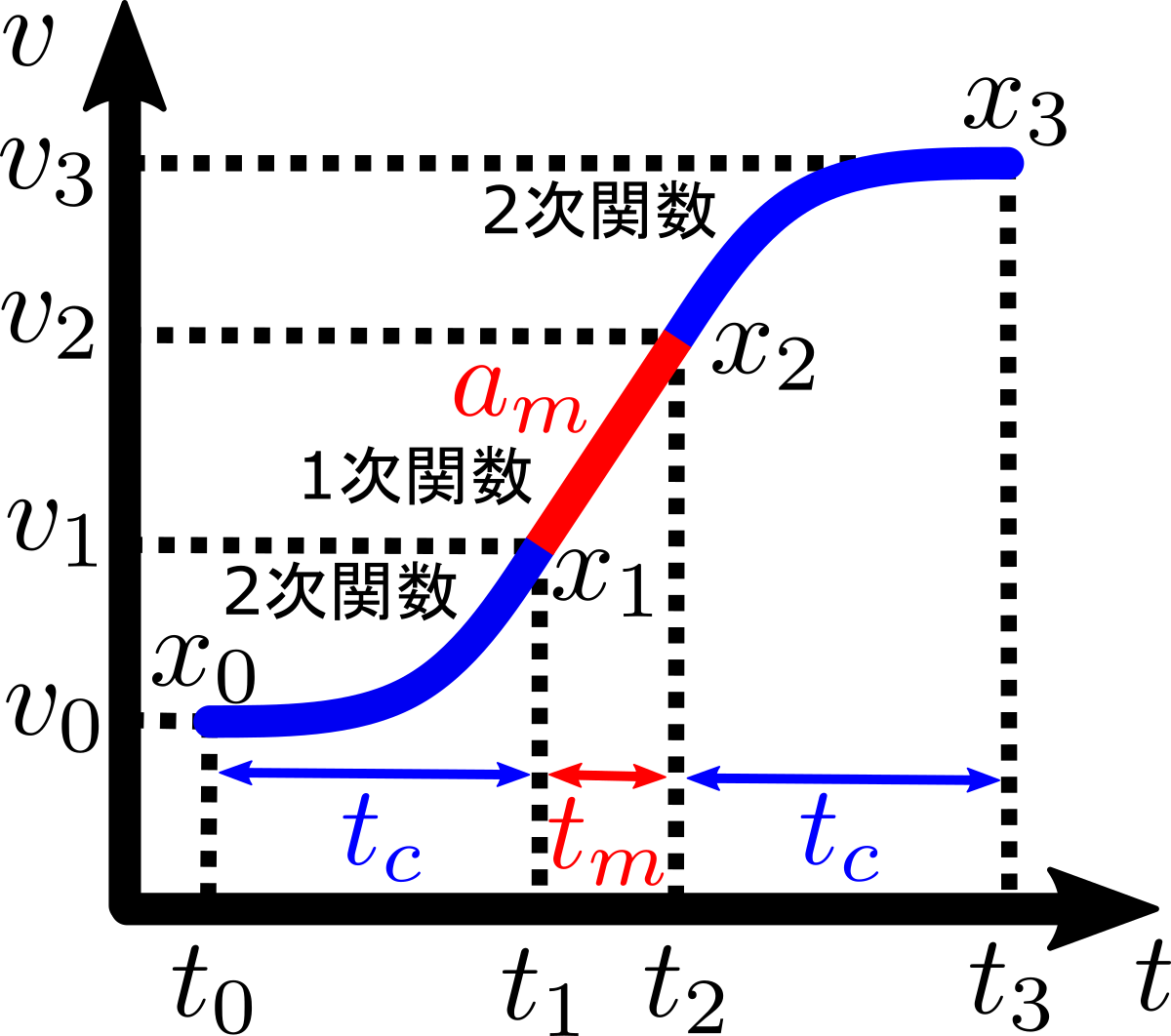
設計2
設計1の曲線を組み合わせて、走行距離に合わせた最適な速度を設計します。
これが実際に走行に使用される曲線加減速となります。
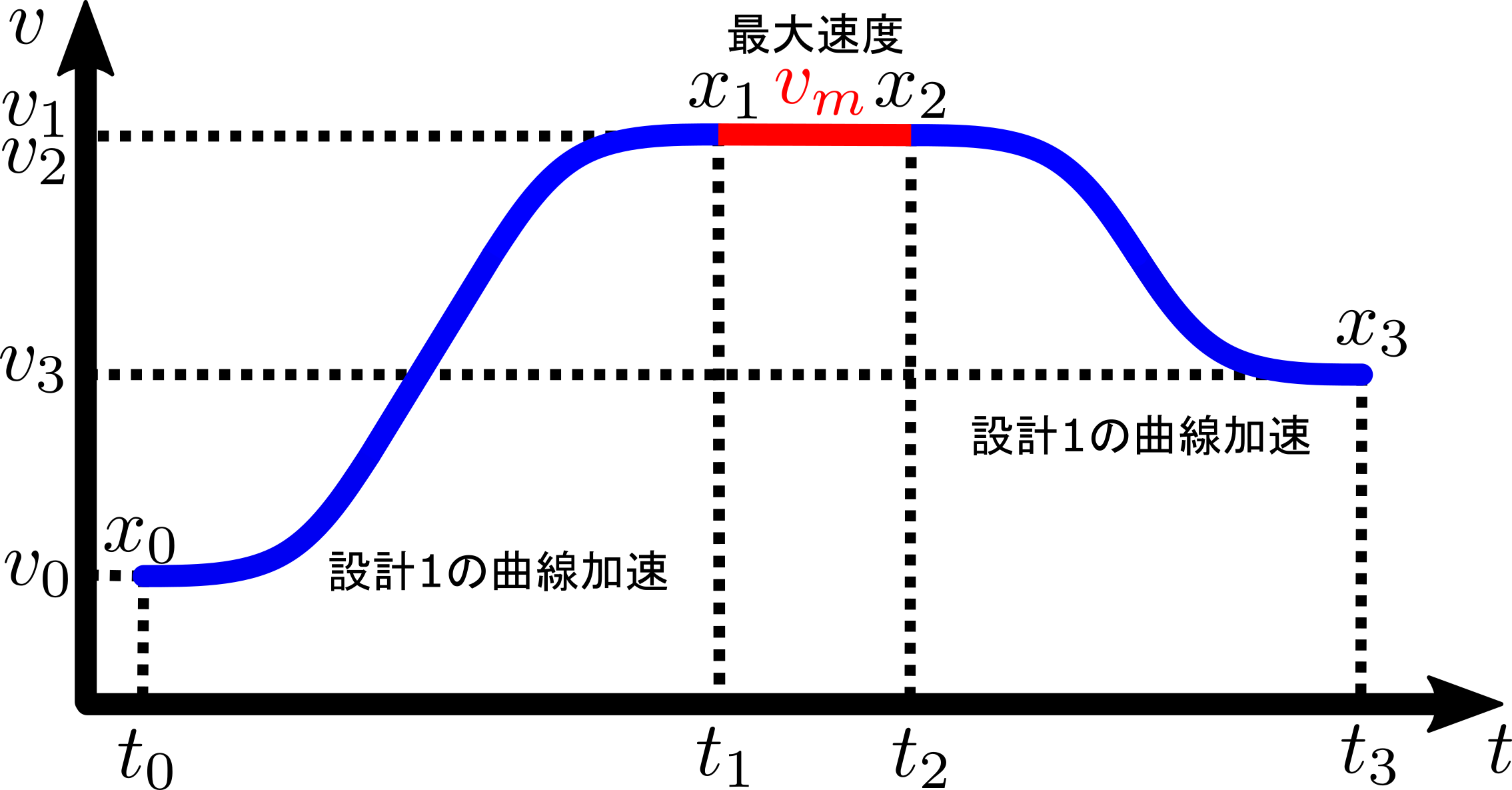
設計2 加減速曲線
まとめ
本記事では、台形加速の問題点を指摘し、曲線加速の必要性を述べました。
次回の記事 では、その曲線加速の設計法を述べていきます。